좋은 관계형 설계의 특징
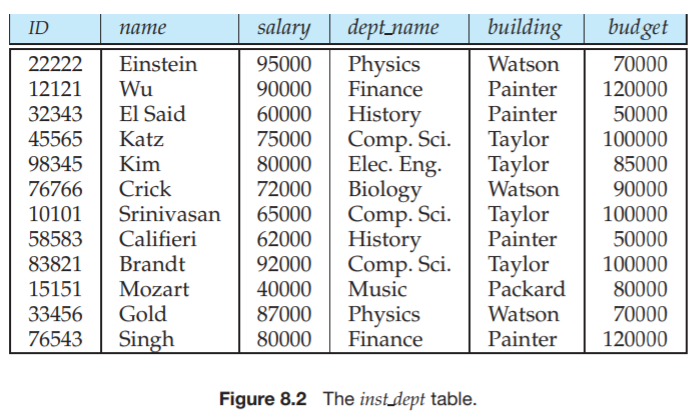
두 릴레이션 instructor와 department를 자연 조인한 inst_dept 하나의 릴레이션으로 결합했다.
그 결과로 같은 학과 내의 교수에 대해서 학과 정보가 반복되게 된다. 이는 일관성 문제를 야기할 수 있다.
따라서 이는 좋지 못한 릴레이션이다.
- 분해(Decomposition)
inst_dept 릴레이션에서 정보의 반복 문제를 해결하는 방법은 inst_dept 릴레이션을 instructor과 department 두 개의 릴레이션으로 분해하는 것이다.
이때 분해된 각 릴레이션은 good form이어야 하고, 분해는 무손실 분해(lossless-join decomposition)여야 한다.
무손실 분해는 함수 종속(functional dependencies)를 이용한다.
함수 종속을 사용한 분해
- 함수 종속(Functional Dependency)
실제 세계의 데이터에는 다양한 제약 조건(constraint)이 존재한다.
예시) 한 학생은 한 과목을 한 번만 수강할 수 있다.
이런 모든 제약 조건을 만족하는 릴레이션의 인스턴스를 적법한 릴레이션이라고 한다.
- 키와 함수 종속
함수 종속은 키라는 개념의 일반화이다.
R이 릴레이션 스키마이고, α ⊆ R, β ⊆ R (α, β는 속성) 라고 하면,
주어진 적법 릴레이션 r(R)에 대해서, 릴레이션 내의 모든 튜플의 쌍 t1, t2에 대해서 "t1[α] = t2[α]이면, t1[β] = t2[β]"이다라는 조건을 만족하면, 함수 종속 α → β를 만족한다고 한다.
예시)

모든 튜플에 대해서 A가 a1이면 C는 c1이고, A가 a2이면 C는 c2이다. 따라서 함수 종속 A → C를 만족한다.
t1 = (a2, b3, c2, d3), t2 = (a3, b3, c2, d4)라고 하면, 두 튜플은 c2라는 동일한 C 값을 가지지만, 각각 다른 A 값 a1, a2를 가진다. 따라서 함수 종속 C → A는 성립되지 않는다.
만약 릴레이션 스키마 R에서 함수 종속 K → R이 성립할 때, K는 수퍼 키라고 한다.
만약 릴레이션 스키마 R에서 함수 종속 K → R이 성립하고, α ⊆ K, α → R을 만족하는 α가 존재하지 않을 때(minimal할 때), K는 후보 키라고 한다.
어떤 함수 종속은 모든 릴레이션이 만족하기 때문에 자명(trivial)하다고 한다.
일반적으로 β ⊆ α이면, α → β가 자명(trivial)하다.
예시)
ID, name → name, name → name
- 손실 분해(Lossy Decomposition)
예시)

어떤 정보가 진짜 정보인지 알 수 없다. 따라서 정보가 손실되었다.
- 무손실 분해(Lossless-join Decomposition)
R을 릴레이션 스키마이고, R1과 R2가 R의 분해라고 하면, 릴레이션 스키마 R에서 가능한 모든 릴레이션 r에 대해 다음을 만족하면, 무손실 분해이다.
$ r = \prod_{R1}(r) \bowtie \prod_{R2}(r) $
함수 종속을 사용하여 어떤 분해가 무손실 분해임을 증명할 수 있다.
R, R1, R2는 릴레이션 스키마이고, F는 함수 종속의 집합이라고 했을 때, 다음과 같은 함수 종속 중 최소한 하나가 $ F^{+} $에 존재하면, R1과 R2는 R의 무손실 분해를 형성한다.
· R1 ∩ R2 → R1
· R1 ∩ R2 → R2
간단히 말해, R1 ∩ R2가 R1 또는 R2에 대한 수퍼 키이면, R을 R1과 R2로 분해하는 것은 무손실 분해이다.
예시)
inst_dept (ID, name, salary, dept_name, building, budget)을 다음과 같이 instru함ctor와 department 스키마로 분해했다.
R1 = instructor (ID, name, dept_name, salary)
R2 = department (dept_name, building, budget)
이때, R1과 R2의 교집합은 dept_name이고, 함수 종속 dept_name → dept_name, building, buget이 성립하므로, 이 분해는 무손실 분해라는 것을 알 수 있다.
함수 종속 이론
- 함수 종속 집합의 폐포(Closure of a Set of Functional Dependencies)
F를 함수 종속 집합이라고 했을 때, F의 폐포(closure)는 $ F^{+} $라고 나타내는데 이는 F에 의해 논리적으로 함축되는 모든 함수 종속의 집합을 의미한다.
$ F^{+} $은 암스트롱의 공리(Armstrong's Axioms)를 적용해 구할 수 있다.
· 만약 β ⊆ α이면, α → β이다. (재귀 규칙, reflexivity)
· 만약 α → β이면, γα → γβ이다. (증가 규칙, augmentation)
· 만약 α → β이고 β → γ이면, α → γ이다. (이행 규칙, transitivity)
이 규칙들은 정당(sound)하고 완전(complete)하다.
예시)

- 속성 집합의 폐포(Closure of Attributes Sets)
주어진 속성 집합 α에 대해서, 함수 종속의 집합 F에서 α에 의해 함수적으로 결정되는 속성의 집합을 F하에서 α에 대한 폐포라고 부르며 $ \alpha^{+} $라고 표시한다.
$ \alpha^{+} $를 구하는 알고리즘은 다음과 같다.

예시)
F = {A → B, B → C, H → J, B → H}에서 $ A^{+} $는?
initial: A
1-loop: AB
1-loop: ABC
1-loop: ABC
1-loop: ABCH
2-loop: ABCH
2-loop: ABCH
2-loop: ABCHJ
2-loop: ABCHJ
3-loop: ABCHJ
3-loop: ABCHJ
3-loop: ABCHJ
3-loop: ABCHJ
$ A^{+} $ = ABCHJ이다.
정규형
- 제1정규형(First Normal Form, 1NF)
만약 릴레이션 스키마 R의 모든 속성의 도메인이 atomic하면, R은 제1정규형(1NF)이다.
예시) non-atomic 도메인
multi-valued attributes, composite attributes
- 보이스-코드 정규형(Boyce-Codd Normal Form, BCNF)
R은 릴레이션 스키마이고, F는 함수 종속의 집합이라 하자.
만약 α ⊆ R이고, β ⊆ R인 α → β 형태의 $ F^{+} $의 모든 함수 종속이 다음 중 적어도 하나라도 만족한다면, 함수 종속의 집합 F와 관련하여 릴레이션 스키마 R은 BCNF에 있다.
· α → β가 자명한(trivial) 함수 종속이다. (즉, β ⊆ α)
· α가 스키마 R의 수퍼 키이다.
예시)
R = (A, B, C)
F = {A → B, B → C}
A → ABC : 수퍼 키이다.
B → BC: 수퍼 키도 아니고, 자명한 함수 종속도 아니다.
따라서 이 릴레이션 스키마는 BCNF가 아니다.
함수 종속을 사용한 분해 알고리즘
- BCNF 분해
릴레이션 스키마 R에 대해서 자명하지 않고, α가 수퍼 키가 아닌 함수 종속 α → β가 BCNF의 위반을 야기한다.
이때, R을 다음과 같이 분해할 수 있다.
· (α ∪ β)
· (R - (β - α))
예시)
inst_dept (ID, name, salary, dept_name, building, budget)
α → β: dept_name →bulding, budget
α = dept_name
β = bulding, budget
inst_dept는 다음 두 개의 릴레이션 스키마로 분해될 수 있다.
R1 = (α ∪ β) = (dept_name, building, budget)
R2 = (R - (β - α)) = (ID, name, salary, dept_name)
이때 R1, R2 각각의 릴레이션 스키마는 BCNF이고, R1 ∩ R2 = (dept_name)은 R1의 수퍼 키 역할을 하므로 무손실 분해이다.
'전공 > 데이터베이스' 카테고리의 다른 글
| 저장 장치 관리 및 인덱싱: 데이터 저장 장치 구조 (0) | 2021.11.26 |
|---|---|
| 저장 장치 관리 및 인덱싱: 물리적 저장 장치 구조 (0) | 2021.11.26 |
| E-R 모델을 사용한 데이터베이스 설계 - (2) (0) | 2021.10.23 |
| E-R 모델을 사용한 데이터베이스 설계 - (1) (0) | 2021.10.20 |
| SQL - (3) (0) | 2021.10.19 |



