데이터베이스 설계 단계
1. 데이터 분석과 요구 사항(requirement)
: 데이터베이스 사용자가 필요로 하는 데이터를 충분히 규정한다.
2. 개념적 설계 단계(conceptual-design phase)
: 데이터 모델을 선택하고, 선택한 데이터 모델의 개념을 적용해 요구 사항을 데이터베이스의 개념 스키마로 변환한다. E-R 모델링은 일반적으로 개념적 설계를 표현한다.
3. 데이터 모델(E-R 모델) 검토
: 스키마를 검토하여 모든 데이터 요구 사항을 만족하고, 서로 충돌하지 않는지 확인하고, 중복되는 사항을 제거한다.
4. 논리적 설계 단계(logical-design phase)
: 상위의 개념 스키마를 사용할 데이터베이스의 구현 데이터 모델에 대응시킨다. 구현 데이터 모델은 일반적으로 관계형 데이터 모델이다.
5. 물리적 설계 단계(physical-design phase)
: 시스템 특유의 데이터베이스 스키마를 이용해 데이터베이스의 물리적 특성을 구체화한다.
개체-관계 모델(Entity-Relationship Model, E-R Model)
- 개체(Entity) 집합
개체는 실세계에서 다른 모든 객체와 구별되는 유무형의 사물이다.
예시) 대학교에서 각 개인 하나의 개체이다.
개체는 속성의 집합을 가지며, 속성 중 일부 집합은 개체를 고유하게 구별하기도 한다.
예시) 개인은 그 사람을 유일하게 구별해주는 person_id라는 속성을 가질 수 있다. 또한 person_id는 특정 개인을 대학교 내에서 유일하게 구분할 수 있다.
개체 집합은 같은 속성을 공유하는 같은 유형의 집합이다.
예시) 어느 대학교의 교수인 사람들의 집합은 개체 집합 instructor로 정의할 수 있다.
- 약한 개체(Weak Entity) 집합
약한 개체 집합은 식별 개체(identifying entity) 집합이라는 다른 개체 집합에 의존하여 존재하는 개체 집합이다.
약한 개체를 주 키와 연결하는 대신, 식별 개체의 주키와 구별자 속성(discriminator attribute)을 함께 사용하여 약한 개체를 유일하게 구분한다. (식별 개체의 주 키 + 구별자 속성 = 약한 개체의 주 키)
약한 개체 집합이 아닌 개체 집합을 강한 개체(strong endity)집합이라 한다.
식별 관계는 약한 개체 집합으로부터 식별 개체 집합으로 다대일 관계이고, 약한 개체 집합은 식별 관계에 전체 참여한다.
E-R 다이어그램에서 구별자 속성은 실선이 아닌 점선으로 밑줄을 긋고, 약한 개체 집합을 식별 개체 집합에 연관 짓는 관계 집합은 이중 다이아몬드로 표현한다.
또한 전체 참여를 표시하기 위해서 이중선을 사용한다.
예시)
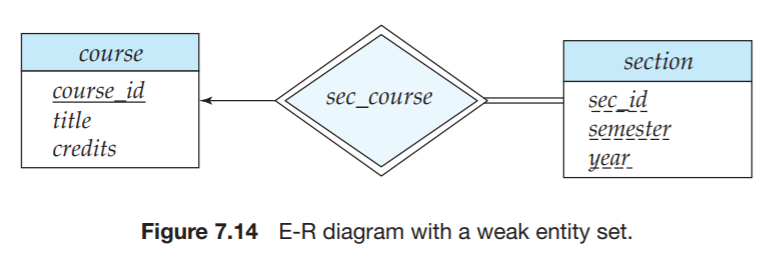
section에 대한 식별 개체 집합은 course이고, section 개체에 상응하는 course 개체에 연관 짓는 식별 관계는 sec_course이다.
section 개체 집합의 주 키는 식별 개체 집합(course)의 주 키와 약한 개체 집합(section)의 구별자를 합하여 만들 수 있다. 따라서 주 키는 {course_id, sec_id, semester, year}이다.
약한 개체 집합 section의 관계 sec_corse에 대한 참여는 전체 참여이므로 이중선으로 표시된다. 이때 전체 참여라는 것은 모든 분반은 반드시 sec_course를 통해 어떤 과목과 연관된다는 것을 의미한다.
sec_course에서 course로 향하는 화살표는 각 분반이 하나의 과목과 연결되어 있다는 것을 표시한다. (course에서 section으로의 일대다 관계이다.)
- 속성(Attribute)
개체는 개체 집합의 모든 개체가 가지는 속성의 집합으로 표현된다.
이때, 각 속성이 가질 수 있는 값의 집합이 존재하는데, 이를 그 속성의 domain 혹은 value set이라고 한다.
E-R 모델에서 속성은 다음과 같은 유형으로 분류된다.
1. 단순(simple) 속성과 복합(composite) 속성
단순 속성은 더 이상 작은 단위로 나뉘지 않는 속성이다.
복합 속성은 더 작은 단위 즉 다른 속성으로 나뉠 수 있는 속성이다.
예시)
name이라는 속성은 first_name, middle_name, last_name으로 구성될 수 있다.
2. 단일값(single-valued) 속성과 다중값(multivalued) 속성
단일값 속성은 특정 개체에 대해서 하나의 값만을 가지는 속성이다.
다중값 속성은 특정 개체에 대해서 값의 집합을 가지는 속성이다.
예시)
instructor 개체 집합의 phone_number이라는 속성은 0개, 1개 혹은 그 이상의 값을 가질 수 있다.
3. 유도(derived) 속성
유도 속성은 다른 관련된 속성이나 개체의 값으로부터 유도된 값을 가지는 속성이다.
예시)instructor 개체 집합의 students_advised 속성의 값은 해당 교수와 관련된 student 개체의 수를 셈으로써 유도할 수 있다.
예시)

name과 address는 복합 속성이다.
phone_number는 다중값 속성으로 "{phone_number}"로 표현된다.
age는 유도 속성이다.
- 중복 속성 제거
instructor와 department 개체 집합을 고려해보자.
instructor 개체 집합은 ID, name, dept_name, salary 속성을 포함하고, ID가 주 키이다.
department 개체 집합은 dept_name, building, budget 속성을 포함하고, dept_name이 주 키이다.
이때, instructor와 department를 연결하는 inst_dept 관계 집합을 이용하여 각각의 교수는 하나의 연관된 학과를 가져야 한다는 사실을 모델링하게 되면, dept_name 속성은 두 개체 집합에 동시에 나타나게 된다.
이 속성은 department 개체 집합의 주 키로 instructor 개체 집합에 중복되어 있으므로 제거될 필요가 있다.
- 관계 집합(Relational Set)
관계는 여러 개체들 사이의 연관성이다.
예시)
교수 Katz와 학생 Shankar를 연결하는 advisor(지도교수)라는 관계를 정의할 수 있다.
관계 집합은 같은 유형의 관계들의 집합이다.
예시)

instructor와 student 두 개체 집합를 생각해 봤을 때, 학생과 지도교수 역할을 하는 교수 사이의 연관성을 표현하기 위해서 관계 집합 advisor를 정의할 수 있다.
관계 집합은 n >= 2개의 개체 집합 사이의 수학적 릴레이션이다.
만약 E1, E2, ... En이 개체 집합일때 관계 집합 R은 {(e1, e2, ..., en) | e1 ∈ E1, e2 ∈ E2, ..., en ∈ En}의 부분집합이다. 여기서 (e1, e2, ..., e3)는 관계 인스턴스이다.
관계 집합은 속성을 가질 수 있다.
예시)
student 개체 집합과 section 개체 집합 사이의 관계 집합 takes는 student의 section에 대한 성적을 기록하기 위해서 grade라는 속성을 추가할 수 있다.
관계 집합에 참여하는 집합의 수를 관계 집합의 차수(degree) 라고 한다.
차수가 1인 관계 집합을 일진(unary) 관계 집합이라 하고, 차수가 2인 관계 집합을 이진(binary) 관계 집합이라하고, 차수가 3인 관계 집합을 삼진(ternary) 관계 집합이라 한다.
예시)

- 대응 카디널리티(Mapping Cardinality)
대응 카디널리티는 관계 집합을 통해 다른 개체와 관련될 수 있는 개체의 수를 나타낸다.
개체 A와 B 사이의 이진 관계 집합에서 대응 카디널리티는 다음 중 하나여야 한다.
1. 일대일(one-to-one)
: A의 한 개체는 B의 최대 하나의 개체와 연관을 가지고, B의 한 개체는 A의 최대 하나의 개체와 연관을 가진다.

2. 일대다(one-to-many)
: A의 한 개체는 임의의 수(0 또는 그 이상)의 B의 개체와 연관을 가지고, B의 한 개체는 A의 최대 하나의 개체와 연관을 가진다.

3. 다대일(many-to-one)
: A의 한 개체는 B의 최대 하나의 개체와 연관을 가지고, B의 한 개체는 임의의 수(0 또는 그 이상)의 A의 개체와 연관을 가진다.

4. 다대다(many-to-many)
: A의 한 개체는 임의의 수(0 또는 그 이상)의 B의 개체와 연관을 가지고, B의 한 개체는 임의의 수(0 또는 그 이상)의 A의 개체와 연관을 가진다.

instructor와 student 개체 집합 사이의 관계 집합에 대해서 일대일, 일대다, 다대다 대응 카디널리티를 다이어그램으로 나타내면 다음과 같다.

(a) 일대일의 경우에는 관계 집합에서 두 개체 집합으로 향하는 화살표를 그린다.
(b) 일대다의 경우에는 관계 집합에서 관계의 '일'쪽으로 화살표를 그린다.
(c) 다대다의 경우에는 관계 집합에서 두 개체 집합으로 향하는 직선을 그린다.
개체 집합 사이의 연관을 참여라고 한다.
두 가지 종류의 참여가 있다.
1. 전체 참여(total participation)
: 개체 집합 E의 모든 개체가 관계 집합 R의 적어도 하나의 관계에 참여할 때, E의 R에 대한 참여를 전체 참여라고 한다.
2. 부분 참여(partial participation)
: 개체 집합 E의 일부 개체는 관계 집합 R의 어떤 관계에 참여하지 않을 수도 있는 경우, E의 R에 대한 참여를 부분 참여라고 한다.
E-R 다이어그램은 관계 집합의 관계에 참여하는 각 개체가 나타나는 횟수에 대한 카디널리티 제약 조건을 나타내는 방법을 제공한다.
카디널리티 제약 조건은 l..h의 형태로 표시한다. 이때 l이 최소 카디널리티이고, h가 최대 카디널리티이다.
최솟값 1은 관계 집합에 있는 개체의 전체 참여를 나타내고, 최댓값 1은 개체가 최대 하나의 관계에 참여함을 나타내고, 최댓값 *은 제한이 없음을 표시한다.
예시)
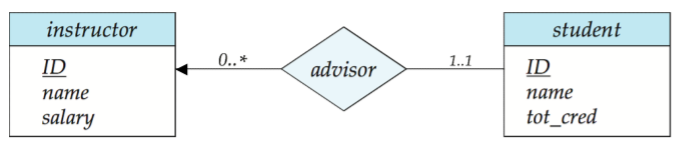
advisor과 student 사이의 선은 카디널리티 제약 조건이 1..1이며, 이는 최소 및 최대 카디널리티가 모두 1임을 의미한다. 즉 각 학생은 정확히 한 명의 지도교수를 가진다.
advisor과 instructor 사이의 선은 카디널리티 제약 조건이 0..*이며, 이는 교수가 지도하는 학생을 한 명도 안가지거나 여러 명을 가질 수 있음을 의미한다.
따라서 관계 advisor는 instructor에서 student로 일대다이고, student는 advisor의 관계에 전체 참여한다.
'전공 > 데이터베이스' 카테고리의 다른 글
| 관계형 데이터베이스 설계 (0) | 2021.10.24 |
|---|---|
| E-R 모델을 사용한 데이터베이스 설계 - (2) (0) | 2021.10.23 |
| SQL - (3) (0) | 2021.10.19 |
| SQL - (2) (0) | 2021.10.19 |
| SQL - (1) (0) | 2021.10.18 |

