peterson의 해결 방법
peterson의 해결 방법은 임계구역에 대한 고전적인 소프트웨어 기반 해결책이다.
이는 현대 컴퓨어에서 제대로 실행된다고 보장할 수 는 없지만,
임계구역 문제 해결을 위한 알고리즘적 설명을 제공하고, 상호 배제, 진행, 한정된 대기의 요구 조건을 다루는 소프트웨어 설계에서의 복잡성을 설명한다.
peterson의 해결 방법은 임계구역과 나머지구역을 번갈아 실행되는 두 프로세스로 제한된다.
peterson의 해결 방법은 두 프로세스가 두 개의 데이터 항목을 공유하도록 하여 해결한다.
int turn;
boolen flag[2];
변수 turn은 임계구역으로 진입할 순번을 나타낸다.
(turn = i이면, Pi가 임계구역에서 실행될 수 있다는 것을 의미한다.)
flag 배열은 프로세스가 임계구역으로 진입할 준비가 되었다는 것을 나타낸다.
(flag[i]가 true이면, Pi가 진입할 준비가 되었다는 것을 의미한다.)
while (true){
flag[i] = true;
turn = j;
while (flag[j] && turn==j)
;
//critical section
flag[i] = false;
//remainder section
}
위 해결책을 상호 배제, 진행, 한정된 대기를 만족하는지 살펴보면 다음과 같다.
1. 상호 배제(mutual exclusion)
flag[0] = flag[1] = 0으로 두 프로세스 모두 임계구역에 들어가기를 원하더라도 turn 값이 순서를 결정하므로 두 프로세스가 동시에 while문을 수행할 수 없다.
따라서 상호 배제가 만족된다.
2. 진행(progress)과 한정된 대기(bounded waiting)
프로세스 Pi가 임계구역을 나오면서 flag[i] = false로 변경하므로,
프로세스 Pi는 다음 임계구역 진입이 불가능하고,
프로세스 Pj가 준비되었다면 임계구역으로 진입하게 된다.
따라서 프로세스는 길어도 1회 대기를 하므로 한정된 대기를 만족하고,
지난번에 진입한 프로세스는 다음 임계구역에 진입이 불가능하므로 진행 또한 만족한다.
peterson의 해결 방법은 현대의 컴퓨터 아키텍처에서 작동한다고 보장되지 않는다.
왜냐하면 시스템 성능 향상을 위해 컴파일러가 읽기 및 쓰기 작업을 재배치할 수 있기 때문이다.
single-threaded 응용 프로그램의 경우에는 정확성 면에서 재배치가 중요하지 않지만,
multithreaded 응용 프로그램에서는 명령어 재배치가 inconsistent하거나 unexpected한 결과를 만들 수 있다.
예시)

예상되는 값은 100이지만, 변수 x와 flag사이에 데이터 종속성이 없으므로 Thread 2에서 x = 100과 flag = true 두 문장을 교환할 수 있다.
이때 출력되는 값은 0으로 예상하지 못한 결과가 나온다.
peterson의 해결 방법의 entry section에 나타나는 첫 두 문장의 순서를 바꾸면 다음과 같은 일이 발생할 수 있다.
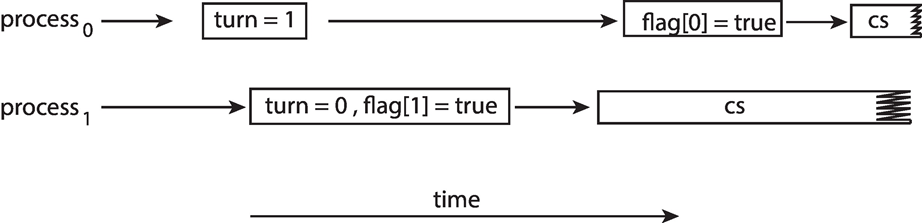
두 스레드가 동시에 임계구역에서 활성화될 수 있다.
따라서 적절한 동기화 도구가 필요하다.
'전공 > 운영체제' 카테고리의 다른 글
| 동기화 도구들: Mutex Locks (0) | 2021.12.16 |
|---|---|
| 동기화 도구들: 동기화를 위한 하드웨어 지원 (0) | 2021.12.16 |
| 동기화 도구들 - (1) (0) | 2021.12.16 |
| CPU 스케줄링: 알고리즘의 평가 - (1) (0) | 2021.12.16 |
| CPU 스케줄링: 실시간 CPU 스케줄링 - (3) (0) | 2021.12.02 |


