관계 대수(Relational Algebra) - 기본 연산자(basic operators)
- 관계 대수(relational algebra)는 한 개 혹은 두 개의 릴레이션을 입력으로 받아 그 결과로 새로운 릴레이션을 생성하는 연산들의 집합으로 구성된다.
- 단항 연산(unary operation): 한 릴레이션에 대해 수행되는 연산
1. 선택 연산(select operation):
주어진 술어(predicate)를 만족하는 튜플을 선택해 주는 단항 연산이다.
선택 술어 내에서 =, ≠, ≤, ≥, <, > 등의 기호를 사용한 비교 연산이 허용된다.
또한 and($ \land $), or($ \lor $), not($ \neg $) 등의 연결 기호를 사용하면 여러 개의 술어를 하나의 큰 술어로 결합할 수 있다.
표기법(notation): $ \sigma _{p}\left ( r \right ) $
예시)

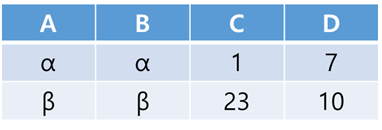
$ \sigma _{(A=B) \wedge (D>5)}(r) $ : A 값이 B 값과 동일하고, D 값이 5 이상인 튜플을 선택한다.
2. 추출 연산(project operation):
입력 릴레이션의 어떤 속성(attribute)을 삭제한 후 나머지 모두를 결과 릴레이션으로 돌려주는 단항 연산이다.
릴레이션은 집합이므로, 어떠한 중복도 제거된다.
표기법(notation): $ \prod _{A_{1}, A_{2}, ..., A_{k}}(r) $
예시)

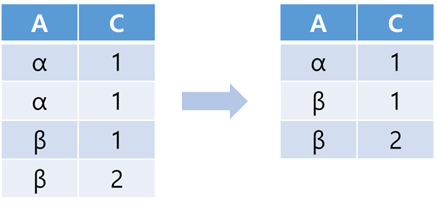
$ \prod _{A, C}(r) $ : A와 C 속성을 추출한다.
3. 재명명 연산(rename operation):
입력 릴레이션의 이름과 속성의 이름을 변경해서 돌려주는 단항 연산이다.
이때, 기존 릴레이션의 이름과 속성의 이름이 바뀌는 것은 아니다.
표기법(notation): $ \rho_{x(A_{1}, A_{2}, ..., A_{n})}(E) $
예시)

$ \rho_{t(M, N, O)}(r) $ : 릴레이션의 이름 r을 t로, 속성 A, B, C를 M, N, O로 재명명한다.

- 이항 연산(binary operation): 한 쌍의 릴레이션에 대해 수행되는 연산
1. 합집합 연산(union operation):
호환 가능(compatible)한 두 릴레이션 중 어느 한쪽 또는 양쪽 모두에 나타나는 튜플을 찾는 이항 연산이다.
이때 호환 가능(compatible)하다는 것은 아래 두 가지 조건을 만족해야 한다는 것이다.
1) 두 릴레이션 r과 s의 속성(attribute)의 개수는 같아야 한다. (same arity)
2) 속성의 도메인이 호환 가능(compatible)해야 한다.
표기법(notation) : $ r \cup s $
예시)

$ r \cup s $ : r과 s 중 한쪽 또는 양쪽 모두에 나타나는 튜플을 찾는다.

2. 차집합 연산(set difference operation):
호환 가능한 두 릴레이션에 대해 한 릴레이션에는 속하고 다른 릴레이션에는 속하지 않는 튜플을 찾는 이항 연산이다.
표기법(notation): r - s
예시)

r - s : r에는 속하고 s에는 속하지 않는 튜플을 찾는다.

3. 카티션 곱 연산(cartesian-product operation):
두 릴레이션의 결합된 정보를 얻는 이항 연산이다.
이때, 두 릴레이션에 같은 이름을 가지는 attribute가 존재하지 않는다고 가정한다.
(만약, 같은 이름을 가지는 attribute가 존재할 경우에는 rename 후 cartesian-product를 적용해야 한다.)
표기법(notation): r × s
예시)
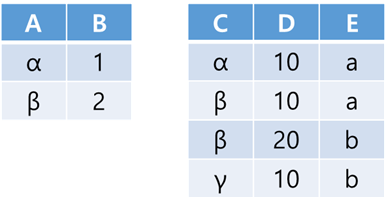
r × s : 두 릴레이션의 결합된 정보를 얻는다.

'전공 > 데이터베이스' 카테고리의 다른 글
| SQL - (2) (0) | 2021.10.19 |
|---|---|
| SQL - (1) (0) | 2021.10.18 |
| 관계형 모델 - (4) (0) | 2021.09.22 |
| 관계형 모델 - (2) (0) | 2021.09.15 |
| 관계형 모델 - (1) (0) | 2021.09.13 |



